Expressions and types

Haskell doesn’t have statements, only expressions
An expression has a value and a type
We write an expression and it’s type like this: expression :: type

Expression	Type	Value
`1+1`	`Int`	`2`
`not True`	`Bool`	`False`

Syntax of expressions

Functions are called by placing the arguments after the function – no special syntax
f 1 is the same as f(1) in other languages
Parenthesis can be used to group expressions (just like in math and other languages)
Function calls bind tighter than operators

Haskell	C
`f 1`	`f(1)`
`f 1 2`	`f(1,2)`
`g f 1`	`g(f,1)`
`g (f 1)`	`g(f(1))`
`a + b`	`a + b`
`f a + g b`	`f(a) + g(b)`
`f (a + g b)`	`f(a+g(b))`
`f a (g b)`	`f(a,g(b))`

Syntax of types

Basic types:

Type	Literals	Use	Operations
`Int`	`1`, `2`, `-3`	The usual number type	`+`, `-`, `*`, `div`, `mod`
`Integer`	`1`, `2`, `900000000000000000`	Unbounded number type	`+`, `-`, `*`, `div`, `mod`
`Double`	`0.1`, `1.2e5`	Floating point numbers	`+`, `-`, `*`, `/`, `sqrt`
`Bool`	`True`, `False`	Truth values	`&&`, `\|\|`, `not`
`String`	`"abcd"`, `""`	Strings of characters	`reverse`, `++`

Functions:
- of one argument: argumentType -> returnType
- of two arguments: arg1Type -> arg2Type -> returnType
- of three arguments: a1 -> a2 -> a3 -> p
- Looks a bit weird right? We’ll get back to this.

The structure of a Haskell program

module Gold where

-- The golden ratio
phi :: Double
phi = (sqrt 5 + 1) / 2

polynomial :: Double -> Double
polynomial x = x^2 - x - 1

f x = polynomial (polynomial x)

main = do
  print (polynomial phi)
  print (f phi)

The structure of a Haskell program

One module per file

module Gold where

A module consists of definitions
A defintion consists of an optional type annotation and one or more equations
Type annotations:

phi :: Double
polynomial :: Double -> Double

Equations for constants and functions:

phi = (sqrt 5 + 1) / 2
f x = polynomial (polynomial x)

Also, comments:

-- The golden ratio

How do I get anything done?

Conditionals
Local definitions
Pattern matching
Recursion

Conditionals

In other languages if is a statement
In Haskell if is an expression
… it corresponds to the ?: operator in C or Java

Java:

int y = (x == 0) ? 3 : x;

Haskell:

y = if x == 0 then 3 else 4

Haskell’s if returns a value. That’s why you always need an else!

Example

factorial n = if n==0
              then 1
              else n * factorial (n-1)

Local definitions

Haskell has two different ways for creating local definitions: let...in and where
NB! these are definitions, not variables. You can’t change them.
where adds local definitions to a definition:

circleArea :: Double -> Double
circleArea r = pi * rsquare
    where pi = 3.1415926
          rsquare = r * r

let...in makes an expression:

circleArea r = let pi = 3.1415926
                   rsquare = r * r
               in pi * rsquare

Local definitions can also be functions:

circleArea r = pi * square r
    where pi = 3.1415926
          square x = x * x

circleArea r = let pi = 3.1415926
                   square x = x * x
               in pi * square r

We’ll get back to the differences between let and where, but mostly you can use which ever you like

Pattern matching

A definition (of a function) can consist of multiple equations
The equations are matched against the arguments until a suitable one is found
We’ll learn more about pattern matching next week!

Examples

greet :: String -> String -> String
greet "Suomi"    name = "Hei. " ++ name
greet "Italia"   name = "Ciao bella! " ++ name
greet "Englanti" name = "How do you do? " ++ name
greet _          name = "Hello. " ++ name

describe :: Integer -> String
describe 0 = "zero"
describe 1 = "one"
describe 2 = "an even prime"
describe n = "the number " ++ show n

funny :: Bool -> Integer -> Integer
funny True 0 = 1
funny True n = n
funny False 0 = 0
funny False 1 = 1
funny False n = -1

Recursion

All sorts of loops are implemented with recursion
Function calls are efficient, don’t worry about performance
Recursion is also a useful way for thinking about solving harder problems

Examples

factorial 0 = 1
factorial n = n * factorial (n-1)

-- compute the sum 1^2+2^2+3^2+...+n^2
squareSum 0 = 0
squareSum n = n^2 + squareSum (n-1)

-- Fibonacci numbers, slow version
fibonacci 1 = 1
fibonacci 2 = 1
fibonacci n = fibonacci (n-2) + fibonacci (n-1)

More recursion

Often you’ll find you need helper variables in recursion
You can get them by defining a helper function
Analogy: arguments of the helper function are variables you update in your loop

Examples

Java:

public int fibonacci(int n) {
    int a = 0;
    int b = 1;
    while (n>1) {
        int c = a+b;
        a=b;
        b=c;
        n--;
    }
    return b;
}

Haskell:

-- fibonacci numbers, fast version
fibonacci :: Integer -> Integer
fibonacci n = fibonacci' 0 1 n

fibonacci' :: Integer -> Integer -> Integer -> Integer
fibonacci' a b 1 = b
fibonacci' a b n = fibonacci' b (a+b) (n-1)

All together now!

module Collatz where

step :: Integer -> Integer
step x = if even x then down else up
  where down = div x 2
        up = 3*x+1

collatz :: Integer -> Integer
collatz 1 = 0
collatz x = 1 + collatz (step x)

longest :: Integer -> Integer
longest upperBound = longest' 0 upperBound

longest' :: Integer -> Integer -> Integer
longest' l 0 = l
longest' l n = if l' > l
               then longest' l' (n-1)
               else longest' l (n-1)
  where l' = collatz n

A word about indentation

The previous examples have been fancily indented
In Haskell indentation matters, a bit like in Python
Rules of thumb
1. Things on the same level start from the same column
2. If an expression has to be split on to many lines, increase indentation

Indentation examples:

These all are ok:

i x = let y = x+x+x+x+x+x in div y 5

j x = let y = x+x+x
              +x+x+x
      in div y 5

k = a + b
  where a = 1
        b = 1

l = a + b
  where
    a = 1
    b = 1

These are not ok:

i x = let y = x+x+x+x+x+x
in div y 5

j x = let y = x+x+x
      +x+x+x
      in div y 5

k = a + b
  where a = 1
      b = 1

l = a + b
where
  a = 1
  b = 1

l = a + b
  where
    a = 1
     b = 1

A word about purity

Haskell is a pure functional language
This means that the value f x y is always the same if the values x and y are the same
- This property is also called referential transparency
This also means that there are no side effects: you can’t have the evaluation f x y print something
Obviously you need side effects to actually get something done. We’ll get back to how Haskell handles side effects on week 3.

Working on the exercises

You can find the exercises in the ifp2018-exercises github repository
- https://github.com/opqdonut/ifp2018-exercises
Read the README.md file in the repository for instructions
For every week you’ll find two files
- W1.hs edit this according to the instructions to complete the exercises
- W1Test.hs run this to check your work
NB! you need to follow the instructions in the file, e.g. “use recursion”. It’s not enough for all tests to pass :)
Return your exercises by email to joel.kaasinen@gmail.com
- Name the files like W1.Surname.hs!
You have roughly 2 weeks to work on each exercise set. Check the course home page for the schedule.

Lecture 2: Catamorphic

Guards
Lists
Functionality
A bit about laziness
A bit about types

Guards

if then else is often a bit cumbersome
An easier alternative is Haskell’s conditional definitions or guarded definitions:

f x y z
  | condition1 x y z = something
  | condition2 x z   = other
  | otherwise        = somethingother

A condition can be any expression of type Bool
The first condition that is True is chosen
otherwise is just an alias for True

Guards: examples

describe :: Int -> String
describe n
  | n==2      = "Two"
  | even n    = "Even"
  | n==3      = "Three"
  | n>100     = "Big!!"
  | otherwise = "The number "++show n

factorial
  | n<0       = -1
  | n==0      = 1
  | otherwise = n * factorial (n-1)

-- guards and pattern matching!
complicated :: Bool -> Double -> Double -> Double
complicated True x y
  | x == y    = 0
  | otherwise = x / (x-y)
complicated False x y
  | y < 0     = sin x
  | otherwise = sin x + sin y

Lists

Literals:

[0,3,4,1+1]

Type: element type in brackets

[True,True,False] :: [Bool]
["Moi","Hei"] :: [String]
[] :: [a] -- more about this later
[[1,2],[3,4]] :: [[Int]]

NB! Lists are homogeneous, which means all the elements must have the same type
Lists are implemented as singly-linked lists. We’ll return to this later

List operations

-- returns the first element
head :: [a] -> a
-- returns everything except the first element
tail :: [a] -> [a]
-- returns the n first elements
take :: Int -> [a] -> [a]
-- returns everything except the n first elements
drop :: Int -> [a] -> [a]
-- lists are catenated with the ++ operator
(++) :: [a] -> [a] -> [a]
-- lists are indexed with the !! operator
(!!) :: [a] -> Int -> a

These operations actually have more generic types, but here I’m pretending that you can only use them on lists:

-- is this list empty?
null :: [a] -> Bool
-- the length of a list
length :: [a] -> Int

Lists can be compared with the familiar == operator
Do you remember?

Prelude> :t "asdf"
"asdf" :: [Char]

String is just an alias for [Char], which means a list of characters
- This means you can use all list operations on strings!

Examples

[7,10,4,5] !! 2
  ==> 4

f xs = take 2 xs ++ drop 4 xs

f [1,2,3,4,5,6]  ==>  [1,2,5,6]
f [1,2,3]        ==>  [1,2]

g xs = tail xs ++ [head xs]

g [1,2,3]      ==>  [2,3,1]
g (g [1,2,3])  ==>  [3,1,2]

A word about type inference and polymorphism

Type variables are types that start with a small letter, e.g. a, b, thisIsATypeVariable
A type variable means a type that is not yet known
- or in other words a type that could be anything
Type variables can turn into concrete types (e.g. Bool) by the process of type inference (also called unification)

Examples of type inference

tail :: [a] -> [a]
tail [True,False] :: [Bool]

head :: [a] -> a
head [True,False] :: Bool

Prelude> [True,False] ++ "Moi"

<interactive>:1:16:
    Couldn't match expected type `Bool' against inferred type `Char'
      Expected type: [Bool]
      Inferred type: [Char]
    In the second argument of `(++)', namely `"Moi"'
    In the expression: [True, False] ++ "Moi"

f xs ys = [head xs, head ys]
g xs = f "Moi" xs

Prelude> :t f
f :: [a] -> [a] -> [a]
Prelude> :t g
g :: [Char] -> [Char]

A word about type annotations

Even though Haskell doesn’t require type annotations, there are multiple reasons to add them:
1. They act as documentation
2. They act as assertions that the compiler checks: help you spot mistakes
3. You can use type annotations to give a function a narrower type than Haskell infers
A good rule of thumb is to give top-level definitions type annotations

Functional programming, at last

In Haskell a function is a value, just like a number or a list is
Functions can be passed as parameters to other functions
Let’s see!

applyTo1 :: (Int -> Int) -> Int
applyTo1 f = f 1

addThree :: Int -> Int
addThree x = x + 3

applyTo1 addThree ==> addThree 1 ==> 1 + 3 ==> 4

More functional programming

That was boring, let’s try something interesting

-- converts a list by applying the given function to the elements
map :: (a -> b) -> [a] -> [b]

map addThree [1,2,3] ==> [4,5,6]

How about this?

-- selects the elements from a list that fulfill a condition
filter :: (a -> Bool) -> [a] -> [a]

positive :: Int -> Bool
positive x = x>0

filter positive [0,1,-1,3,-3] ==> [1,3]

Even more functional programming

How many “palindrome numbers” are between 1 and n

palindromes n = filter palindrome (map show [1..n])
  where palindrome str = str == reverse str

length (palindromes 9999) ==> 198

Which contexts of length k follow the character c in the string s?

-- These are from the Data.List module in the standard library
tails :: [a] -> [[a]]        -- return a list of suffixes of a given list
sort :: Ord a => [a] -> [a]  -- sorts a list

contexts :: Int -> Char -> String -> [String]
contexts k c s = sort (map tail (filter match (map process (tails s))))
  where match [] = False
        match (c':_) = c==c'
        process x = take (k+1) x

contexts 2 'a' "abracadabra" ==> ["","br","br","ca","da"]

Partial application

Defining all those helper functions was a bit of a chore
Luckily Haskell’s functions behave a bit weirdly…

f :: Bool -> Integer -> Integer -> Integer -> Integer
f True  x _ z = x+z
f False _ y z = y+z

Let’s give f less arguments than it needs:

Prelude> (f True) 1 2 3
4
Prelude> let g = (f True) in g 1 2 3
4
Prelude> let g = (f True 1) in g 2 3
4
Prelude> map (f True 1 2) [1,2,3]
[2,3,4]

Types:

Prelude> :t f True
f True :: Integer -> Integer -> Integer -> Integer
Prelude> :t f True 1
f True 1 :: Integer -> Integer -> Integer
Prelude> :t f True 1 2
f True 1 2 :: Integer -> Integer
Prelude> :t f True 1 2 3
f True 1 2 3 :: Integer

Partial application 2

BTW, this also works with operators

Prelude> map (*2) [1,2,3]
[2,4,6]
Prelude> map (2*) [1,2,3]
[2,4,6]
Prelude> map (1/) [1,2,3,4,5]
[1.0,0.5,0.3333333333333333,0.25,0.2]

The `.` operator

Here’s a couple of operators that help in writing functional code
Function composition: .

(.) :: (b -> c) -> (a -> b) -> a -> c

It works like this

(f.g) x ==> f (g x)

Examples:

double x = 2*x
quadruple = double . double  -- computes 2*(2*x) == 4*x
f = quadruple . (+1)         -- computes 4*(x+1)

third = head . tail . tail   -- fetches the third element of a list

The `$` operator

The $ operator is more subtle

($) :: (a -> b) -> a -> b

It does nothing, but it has a very low precedence so it can be used to eliminate parentheses!
f x y z $ g z w is the same as (f x y z) (g z w)
With both of these operators, we can rewrite

f x (g y (h x y (i z z)))

f x . g y . h x y $ i z z

Witness:

        f x . g y . h x y $ i z z
  ==>  (f x . g y . h x y) (i z z)
  ==>  (f x . g y) (h x y  (i z z))
  ==>  (f x  (g y  (h x y  (i z z))))

Lambdas

The last spanner we need in this tool set is λ (lambda)
Lambda expressions are anonymous functions

Prelude> (\x -> x*x) 3
9
Prelude> (\x -> reverse x == x) "ABBA"
True
Prelude> filter (\x -> reverse x == x) ["ABBA","ACDC","otto","lothar","anna"]
["ABBA","otto","anna"]
Prelude> (\x y -> x^2+y^2) 2 3
13

In general

\x0 x1 x2 ... -> e

is the same as

let f x0 x1 x2 ... = e in f

Functional style

Let’s rewrite the contexts function using ., $ and lambdas
Original:

contexts :: Int -> Char -> String -> [String]
contexts k c s = sort (map tail (filter match (map process (tails s))))
  where match [] = False
        match (c':_) = c==c'
        process x = take (k+1) x

Use partial application instead of process:

contexts k c s = sort (map tail (filter match (map (take (k+1)) (tails s))))
  where match [] = False
        match (c':_) = c==c'

Use . and $ to eliminate parentheses:

contexts k c s = sort . map tail . filter match . map (take $ k+1) $ tails s
  where match [] = False
        match (c':_) = c==c'

Use partial application to replace match:

contexts k c = sort . map tail . filter ((==[c]).take 1) . map (take $ k+1) . tails

Mic drop

More functional list wrangling examples

-- find the first substring that consists only of the given characters
findSubString :: [String] -> [String] -> [String]
findSubString chars = takeWhile (\x -> elem x chars)
                      . dropWhile (\x -> not $ elem x chars)

findSubString "abcd" "xxxyyyzabaaxxabcd"  ==>  "abaa"

-- split the string into pieces at the given character
split :: Char -> [String] -> [[String]]
split c [] = []
split c xs = start : split c (drop 1 rest)
  where start = takeWhile (/=c) xs
        rest = dropWhile (/=c) xs

split 'x' "fooxxbarxquux"   ==>   ["foo","","bar","quu"]

… and more!

-- from the module Data.Ord
-- compares two values "through" the function f
comparing :: (Ord a) => (b -> a) -> b -> b -> Ordering
comparing f x y = compare (f x) (f y)

-- from the module Data.List
-- sorts a list using the given comparison function
sortBy :: (a -> a -> Ordering) -> [a] -> [a]

-- sorts lists by their length
sortByLength :: [[a]] -> [[a]]
sortByLength = sortBy (comparing length)

sortByLength [[1,2,3],[4,5],[4,5,6,7]]   ==>  [[4,5],[1,2,3],[4,5,6,7]]

Colon

Here’s a new operator, :

Prelude> 1:[]
[1]
Prelude> 1:[2,3]
[1,2,3]
Prelude> tail (1:[2,3])
[2,3]
Prelude> head (1:[2,3])
1
Prelude> :t (:)
(:) :: a -> [a] -> [a]

: builds a list, out of a head and a tail
: is actually the constructor for lists: it returns a new linked list node
Here’s a picture of how [1,2,3] is structured:

   (:)
  /   \
 1    (:)
     /   \
    2    (:)
        /   \
       3    []

Building a list

Now we can define recursive functions that build lists

descend 0 = []
descend n = n : descend (n-1)

descend 4 ==> [4,3,2,1]

iterate f 0 x = [x]
iterate f n x = x : iterate f (n-1) (f x)

iterate (*2) 4 3 ==> [3,6,12,24,48]

let xs = "terve"
in iterate tail (length xs) xs
  ==> ["terve","erve","rve","ve","e",""]

Pattern matching for lists

Since : is a constructor, we can pattern match it
- (more about constructors later)
The other list constructor is [], the empty list

myhead :: [Int] -> Int
myhead [] = -1
myhead (first:rest) = first

mytail :: [Int] -> [Int]
mytail [] = []
mytail (first:rest) = rest

You can nest patterns. Also, (a:b:_) is the same as (a:(b:_)):

sumFirstTwo :: [Integer] -> Integer
sumFirstTwo (a:b:_) = a+b
sumFirstTwo _       = 0

Consuming a list

Using pattern matching, we can define a (recursive) function that processes a whole list

sumNumbers :: [Int] -> Int
sumNumbers [] = 0
sumNumbers (x:xs) = x + sumNumbers xs

myMaximum :: [Int] -> Int
myMaximum [] = 0       -- actually this should be some sort of error...
myMaximum (x:xs) = go x xs
  where go biggest [] = biggest
        go biggest (x:xs) = go (max biggest x) xs

sum2d :: [[Int]] -> Int
sum2d []           = 0
sum2d ([]:xss)     = sum2d xss
sum2d ((x:xs):xss) = x + sum2d (xs:xss)

Building and consuming a list

Now that we can build and consume lists, let’s do both of them:

doubleList :: [Int] -> [Int]
doubleList [] = []
doubleList (x:xs) = 2*x : doubleList xs

It evaluates like this:

doubleList [1,2,3]
==> doubleList (1:(2:(3:[])))
==> 2*1 : doubleList (2:(3:[]))
==> 2*1 : (2*2 : doubleList (3:[]))
==> 2*1 : (2*2 : (2*3 : doubleList []))
==> 2*1 : (2*2 : (2*3 : []))
=== [2*1, 2*2, 2*3]
==> [2,4,6]

Building and consuming a list continued

Here’s the GHC implementation for map:

map :: (a -> b) -> [a] -> [b]
map _ []     = []
map f (x:xs) = f x : map f xs

and for filter:

filter :: (a -> Bool) -> [a] -> [a]
filter _pred []    = []
filter pred (x:xs)
  | pred x         = x : filter pred xs
  | otherwise      = filter pred xs

Infinite lists

To demonstrate Haskell’s laziness, here are some examples with infinite lists!

Prelude> repeat 1
[1,1,1,1,
^C
Prelude> take 10 $ repeat 1
[1,1,1,1,1,1,1,1,1,1]
Prelude> take 20 $ repeat 1
[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
Prelude> repeat 1 !! 13337
1

Prelude> take 10 . map (2^) $ [0..]
[1,2,4,8,16,32,64,128,256,512]

Prelude> take 21 $ cycle "asdf"
"asdfasdfasdfasdfasdfa"
Prelude> take 4 . map (take 4) . tails $ cycle "asdf"
["asdf","sdfa","dfas","fasd"]

This runs in constant memory:

Prelude> head . filter (>10^8) $ map (3*) [0..]
100000002

Laziness & Purity

Laziness means that a value is not evaluated if it is not needed

f x = f x   -- infinite recursion
g x y = x

This does not halt:

f 1

But this works:

g 2 (f 1)  ==>  2

Laziness is not a problem because Haskell is pure
- Only the result of the function matters, not the side effects

Laziness Example

Laziness explains why this works:

Prelude> head . filter (>100) $ map (3^) [0..]
243

Let’s evaluate!

    head (filter (>100) (map (3^) [0..]))
==> head (filter (>100) (map (3^) (0:[1..])))
==> head (filter (>100) (1 : map (3^) [1..]))
==> head (filter (>100) (map (3^) [1..]))
==> head (filter (>100) (map (3^) (1:[2..])))
==> head (filter (>100) (3 : map (3^) [2..]))
==> head (filter (>100) (map (3^) [2..]))
-- let's take bigger steps now
==> head (filter (>100) (9 : map (3^) [3..]))
==> head (filter (>100) (27 : map (3^) [4..]))
==> head (filter (>100) (81 : map (3^) [5..]))
==> head (filter (>100) (243 : map (3^) [6..]))
==> head (243 : filter (>100) (map (3^) [6..]))
==> 243

More about how Haskell evaluation works in a future lecture

Lecture 3: You Need String for a Knot

Type system
Defining custom types

Algebraic Datatypes: Introduction

Here are the standard library definitions for the familiar types Bool and Ordering:

data Bool = True | False
data Ordering = LT | EQ | GT

With this syntax you too can define types:

data Color = Red | Green | Blue

rgb :: Color -> [Double]
rgb Red = [1,0,0]
rgb Green = [0,1,0]
rgb Blue = [0,0,1]

Prelude> :t Red
Red :: Color
Prelude> :t [Red,Blue,Green]
[Red,Blue,Green] :: [Color]
Prelude> rgb Red
[1.0,0.0,0.0]

Algebraic Datatypes: Fields

The data syntax can be used for other kinds of datatypes as well. Here we define a report type that contains an id number, a title, and a body:

data Report = MkReport Int String String

This is how you create a report:

Prelude> :t MkReport 1 "a" "b"
MkReport 1 "a" "b" :: Report

You can access the fields with pattern matching:

reportContents :: Report -> String
reportContents (MkReport id title contents) = contents
setReportContents :: String -> Report -> Report
setReportContents contents (MkReport id title _contents) = MkReport id title contents

Algebraic Datatypes: Constructors

The things on the right hand side of a data declaration are called constructors
- True, False, LT, MkReport, …
Multiple constructors can be defined using the | syntax
Here is a datatype for a standard playing card:

data Card = Joker | Heart Int | Club Int | Spade Int | Diamond Int

Constructors are functions:

Prelude> :t Heart
Heart :: Int -> Card
Prelude> :t Club
Club :: Int -> Card

They can be used like functions:

Prelude> map Heart [1,2,3]
[Heart 1,Heart 2,Heart 3]
Prelude> (Heart . succ) 3
Heart 4

`deriving Show`

Oh, by the way

Prelude> EQ
EQ
Prelude> True
True
Prelude> Joker
<interactive>:1:0:
    No instance for (Show Card)
      arising from a use of `print' at <interactive>:1:0-4
    Possible fix: add an instance declaration for (Show Card)
    In a stmt of a 'do' expression: print it

GHC does not know how to print the types we defined
The easy solution is to use deriving Show:

data Card = Joker | Heart Int | Club Int | Spade Int | Diamond Int
  deriving Show

Prelude> Joker
Joker

We’ll learn more about deriving and what Show is later

Example 1: Maybe I’m Amazed

Sometimes an operation doesn’t have a valid return value. (E.g. division by zero.) We have a couple of options
- Use the wrong value, like -1 – ugly, not always possible
- Throw an exception - impure
- The Maybe type – pure and safe
Maybe a is the type with the values Nothing and Just x, where x :: a

Type	Values
`Maybe Bool`	`Nothing`, `Just False`, `Just True`
`Maybe Int`	`Nothing`, `Just 0`, `Just 1`, …
`Maybe [Int]`	`Nothing`, `Just []`, `Just [1,1337]`, …

You can think of Maybe a as being a bit like [a] except there can only be 0 or 1 elements, not more.

Example 1: continued

Using Maybe is easy. Just pattern match:

intOrZero :: Maybe Int -> Int
intOrZero Nothing = 0
intOrZero (Just i) = i

safeHead :: [a] -> Maybe a
safeHead [] = Nothing
safeHead (x:_) = Just x

headOrZero :: [Int] -> Int
headOrZero xs = case safeHead xs of Nothing -> 0
                                    Just x -> x

The definition for Maybe is:

data Maybe a = Nothing | Just a

what’s a? We’ll find out next.

Algebraic Datatypes: type parameters

Haskell types can have other types as parameters
This is a bit like Java Generics or C++ templates
- Compare: Maybe Integer, Optional<Integer>
The simplest example:

data Wrap a = MkWrap a
unwrap (MkWrap a) = a

Prelude> :t MkWrap
MkWrap :: a -> Wrap a
Prelude> :t unwrap
unwrap :: Wrap a -> a
Prelude> :t MkWrap True
MkWrap True :: Wrap Bool
Prelude> :t MkWrap []
MkWrap [] :: Wrap [a]

Remember:

data Maybe a = Nothing | Just a

Syntactic note

Type variables and names for functions and values start lower case:
- a, map, xs, …
Type names and constructor names start with upper case:
- Maybe, Just, Card, Heart, …
Beware of mixing types and constructors (especially since they can have the same name):

data Wrap a = Wrap a
data Report = Report Int String String

But luckily types and constructors can never occur in the same context:

Prelude> Maybe
<interactive>:1:1: error:
    • Data constructor not in scope: Maybe

Prelude> undefined :: Nothing
<interactive>:2:14: error:
    Not in scope: type constructor or class ‘Nothing’

Example 2: Either you die a hero…

Sometimes it would be nice if you could add an error message or something to Nothing
That’s why we have Either:

data Either a b = Left a | Right b

Maybe a let us return a value of type a or nothing
Either a b lets us return a value of type a or a value of type b
NB! Two type parameters
Simple example: reporting an error

readInt :: String -> Either String Int
readInt "0" = Right 0
readInt "1" = Right 1
readInt s = Left ("Unsupported string "++show s)

Another example: pattern matching an Either

iWantAString :: Either Int String -> String
iWantAString (Right str)   = str
iWantAString (Left number) = show number

Example 2: continued

Using Either to signal when to stop iterating

iterateE :: (a -> Either b a) -> a -> b
iterateE f x = case f x of Left y  -> y
                           Right y -> iterateE f y

step :: Int -> Int -> Either Int Int
step k x = if x>k then Left x else Right (2*x)

goThru :: [a] -> Either a [a]
goThru [x] = Left x
goThru (x:xs) = Right xs

Prelude> iterateE (step 100) 1
128
Prelude> iterateE (step 1000) 3
1536
Prelude> iterateE goThru [1,2,3,4]
4

Algebraic Datatypes: recursion

Just like functions, data types can be recursive
This is no weirder than having an object that refers to another object of the same class
Example: a list of integers

data IntList = Empty | Node Int IntList
  deriving Show

ihead :: IntList -> Int
ihead (Node i _) = i

itail :: IntList -> IntList
itail (Node _ t) = t

ilength :: IntList -> Int
ilength Empty = 0
ilength (IntList _ t) = 1 + ilength t

Example 3: Let me list the ways

Let’s do the same thing with a type parameter
This is the same as the built in type [a]

data List a = Empty | Node a (List a)
  deriving Show

lhead :: List a -> a
lhead (Node h _) = h

ltail :: List a -> List a
ltail (Node _ t) = t

lnull :: List a -> Bool
lnull Empty = True
lnull _     = False

llength :: List a -> Int
llength Empty = 0
llength (Node _ t) = 1 + llength t

Example 4: Growing a tree

Just like a list, we can also represent a binary tree:

data Tree a = Leaf | Node a (Tree a) (Tree a)

Our tree contains
- leafs, in other words empty trees: Leaf
- nodes, which contain a value of type a and two child trees
Example: computing the height of a tree

treeHeight :: Tree a -> Int
treeHeight Leaf = 0
treeHeight (Node _ l r) = 1 + max (treeHeight l) (treeHeight r)

treeHeight Leaf ==> 0
treeHeight (Node 2 Leaf Leaf)
  ==> 1 + max (treeHeight Leaf) (treeHeight leaf)
  ==> 1 + max 0 0
  ==> 1
treeHeight (Node 1 Leaf (Node 2 Leaf Leaf))
  ==> 1 + max (treeHeight Leaf) (treeHeight (Node 2 Leaf Leaf))
  ==> 1 + max 0 1
  ==> 2
treeHeight (Node 0 (Node 1 Leaf (Node 2 Leaf Leaf)) Leaf)
  ==> 1 + max (treeHeight (Node 1 Leaf (Node 2 Leaf Leaf))) (treeHeight Leaf)
  ==> 1 + max 2 0
  ==> 3

Example 4: continued

Additional example: binary tree search and insertion

insert :: Int -> Tree Int -> Tree Int
insert x Leaf = Node x Leaf Leaf
insert x (Node y l r)
  | x < y = Node y (insert x l) r
  | x > y = Node y l (insert x r)
  | otherwise = Node y l r

lookup :: Int -> Tree Int -> Bool
lookup x Leaf = False
lookup x (Node y l r)
  | x < y = lookup x l
  | x > y = lookup x r
  | otherwise = True

Algebraic Datatypes: Summary

Types are defined like this

data TypeName = ConstructorName FieldType FieldType2 | AnotherConstructor FieldType3 | OneMoreCons

… or like this if we’re using type variables

data TypeName variable = Cons1 variable Type1 | Cons2 Type2 variable

You can have one or more constructors
Each constructor can have zero or more fields
Constructors start with upper case, type variables with lower case
Values are handled with pattern matching:

foo (ConstructorName a b) = a+b
foo (AnotherConstructor _) = 0
foo OneMoreCons = 7

Constructors are just functions:

ConstructorName :: FieldType -> FieldType2 -> TypeName
Cons1 :: a -> Type1 -> TypeName a

Immutability

Haskell data structures form graphs in memory
Every constructor is a node, every field is an edge
Structure can be shared

     code                       memory
                          x             y
                          |             |
let x = [1,2,3,4]        (1:) - (2:) - (3:) - (4:) - []
    y = drop 2 x                       /
    z = 5:y                    z - (5:)

Path copying

This means all changes must copy parts of the graph, this is called path copying
Consider the definition of ++:

[]     ++ ys = ys
(x:xs) ++ ys = x:(xs ++ ys)

We are making a copy of the first argument while we walk it
The second argument can be shared

      xs - (1:) - (2:) - (3:) - []

                         ys - (5:) - (6:) - []
                             /
xs ++ ys - (1:) - (2:) - (3:)

Path copying: contd.

Final example: binary tree insertion

insert :: Int -> Tree Int -> Tree Int
insert x Leaf = Node x Leaf Leaf
insert x (Node y l r)
  | x < y = Node y (insert x l) r
  | x > y = Node y l (insert x r)
  | otherwise = Node y l r

          t              insert 6 t
          |                  |
        Node 5            Node 5
       /______\__________/      \
      //       \                 \
 Node 3        Node 7            Node 7
 /    \        /    \           /      \
Leaf  Node 4  Leaf  Leaf    Node 6    Leaf
     /    \                /     \
   Leaf   Leaf           Leaf   Leaf

Something fun: Tying the Knot

Recursion combined with sharing gives us cyclic structures
Also known as tying the knot

  code             memory
let xs = 1:2:xs      xs - (1:) - (2:) -+
 in xs                     |           |
                           +-----------+

      code                                           memory
-- a Coin with a text and a flip side
data Coin = Side String Coin                  dollar
                                                |
dollar :: Coin                               Side "heads" --+
dollar = heads                                      ^       |
  where heads = Side "heads" tails                  |       v
        tails = Side "tails" heads                  +-- Side "tails"

Something fun: list comprehensions

Haskell has a nice syntax for defining lists that combines map and filter:

[2*i | i<-[1,2,3]]
  ==> [2,4,6]

let f = (2*)
    lis = [0..10]
in [f x | x<-lis]
  ==> [0,2,4,6,8,10,12,14,16,18,20]

[(x,y) | x <- [1..7], even x, y <- [True,False]]
  ==> [(2,True),(2,False),(4,True),(4,False),(6,True),(6,False)]

These are equivalent:

[f x | x <- lis, p x]
map f (filter p lis)

Something fun: custom operators

In Haskell an operator is anything built from the characters !#$%&*+./<=>?@\^|-~
Operators can be defined just like functions (note the slightly different type annotation):

(<+>) :: [Int] -> [Int] -> [Int]
xs <+> ys = zipWith (+) xs ys

(+++) :: String -> String -> String
a +++ b = a ++ " " ++ b

Functions can be used as operators with the `foo`-syntax:

Prelude> 5 `div` 2
2
Prelude> (+1) `map` [1,2,3]
[2,3,4]

Lecture 4: `RealWorld -> (a,RealWorld)`

Oh right: `case of`

Here’s how the case of expression that’s been mentioned a couple of times works:

case expression of
  pattern -> expression
  pattern -> expression

For example:

myHead :: [Int] -> Int
myHead xs = case xs of (x:_) -> x
                       []    -> -1

You’ve been fooled

Actually Haskell is the world’s best imperative programming language!
Let’s start:

questionnaire = do
  putStrLn "Write something!"
  s <- getLine
  putStrLn $ "You wrote: "++s

import Network.HTTP
import Control.Monad

main = do
  rsp <- Network.HTTP.simpleHTTP $ getRequest "http://pseudo.fixme.fi/~opqdonut/ifp2018/words"
  s <- getResponseBody rsp
  forM_ (words s) $ \s -> do
     putStrLn "word:"
     putStrLn s

What’s going on?

Prelude> :t putStrLn
putStrLn :: String -> IO ()
Prelude> :t getLine
getLine :: IO String

IO a is an operation that produces a value of type a
() is the so called unit type, its only value is ()
So:

Haskell type	Java-type
`foo :: IO ()`	`void foo()`
`bar :: IO a`	`a bar()`
`f :: a -> b -> IO ()`	`void f(a arg0, b arg1)`
`g :: c -> IO d`	`d g(c arg)`

`do` as thou wilt

These IO operations can be combined into bigger operations using the do syntax:

do operation
   operation arg
   variable <- operationThatReturnsStuff
   let var2 = expression
   operationThatProducesTheResult var2

Examples

You can find useful IO operations in the standard library modules Prelude and System.IO

query :: IO ()
query = do
  putStrLn "Write something!"
  s <- getLine
  let n = length s
  putStrLn $ "You wrote "++show n++" characters: "++s

returningQuery :: String -> IO String
returningQuery question = do
  putStrLn question
  getLine

`return`

return takes a value and turns it into an operation, that returns that value

produceThree :: IO Int
produceThree = return 3

printThree :: IO ()
printThree = do
  three <- produceThree
  putStrLn $ show three

Doesn’t sound useful? Combined with do it is:

yesNoQuestion :: String -> IO Bool
yesNoQuestion question = do
  putStrLn question
  s <- getLine
  return $ s == "Y"

`return` pitfalls

ATTENTION! return does not stop execution of an operation (unlike return in Java or C)
return is a function that takes a value and returns an operation. Nothing else.
In do-notation, the last line decides which value to produce
so this produces 2:

do return 1
   return 2

Also note that that these are the same:

do ...
   x <- op
   return x

do ...
   op

Since return is a function, you should remember to parenteshize any complex expressions

return (f x : xs)
-- alternatively:
return $ f x : xs

`do` and types

do builds a value of type IO <something>

Example 1

foo = do
  ...
  lastOp

lastOp must be of type IO X
The type of foo will also be IO X

Example 2

foo x y = do
  ...
  lastOp arg

lastOp must be of type Y -> IO X
The type of foo will be A -> B -> IO X (for x :: A and y :: B)

Example 3

foo x = do
  ...
  return arg

foo will have type A -> IO B, where x :: A and arg :: B

Control structures 1

The usual tools of recursion, guards and if-then-else also work in the IO world

printDescription :: Int -> IO ()
printDescription n
  | even n    = putStrLn "even"
  | n==3      = putStrLn "three"
  | otherwise = print n

readAndSum :: Int -> IO Int
readAndSum 0 = return 0
readAndSum n = do
  i <- readLn
  s <- readAndSum (n-1)
  return $ i+s

ask :: [String] -> IO [String]
ask [] = return []
ask (question:questions) = do
  putStr question
  putStrLn "?"
  answer <- getLine
  answers <- ask questions
  return $ answer:answers

Control structures 2

Additionally, we have some IO-specific control structures (in the module Control.Monad)

-- conditional operation
when :: Bool -> IO () -> IO ()
-- conditonal operation, vice versa
unless :: Bool -> IO () -> IO ()
-- do something many times
replicateM :: Int -> IO a -> IO [a]
-- do something many times, throw away the results
replicateM_ :: Int -> IO a -> IO ()
-- do something for every list element
mapM :: (a -> IO b) -> [a] -> IO [b]
-- do something for every list element, throw away the results
mapM_ :: (a -> IO b) -> [a] -> IO ()
-- the same, but arguments flipped
forM  :: [a] -> (a -> IO b) -> IO [b]
forM_ :: [a] -> (a -> IO b) -> IO ()

readAndSum n = do
  numbers <- replicateM n readLn
  return $ sum numbers

ask :: [String] -> IO [String]
ask questions = do
  forM questions $ \question -> do
    putStr question
    putStrLn "?"
    getLine

Useful operations

Input/output:

-- printing
putStr :: String -> IO ()
putStrLn :: String -> IO ()
print :: Show a => a -> IO ()
print = putStr . show
-- reading
getLine :: IO String
readLn :: Read a => IO a

Files (from the module System.IO):

-- simple operations:
-- FilePath is just String
readFile :: FilePath -> IO String
writeFile :: FilePath -> String -> IO ()
-- with file handles:
openFile :: FilePath -> IOMode -> IO Handle   -- IOMode is either ReadMode, WriteMode, or ReadWriteMode
hPutStr :: Handle -> String -> IO ()
hPutStrLn :: Handle -> String -> IO ()
hPrint :: (Show a) => Handle -> a -> IO ()
hGetLine :: Handle -> IO String
-- etc

String processing

Here are a couple of useful string processing functions:

-- split a string into lines
lines :: String -> [String]
-- build a string out of lines
unlines :: [String] -> String
-- split a string into words
words :: String -> [String]
-- build a string out of words
unwords :: [String] -> String
-- render a value into a string
show :: Show a => a -> String
-- read a string into a value (opposite of show!)
read :: Read a => String -> a

Let’s do something real

Fetch all type annotations from all .hs files under this directory:

-- a line is a type signature if it contains :: but does not contain =
isTypeSignature :: String -> Bool
isTypeSignature s = not (isInfixOf "=" s) && isInfixOf "::" s

-- return list of types for a .hs file
readTypesFile :: FilePath -> IO [String]
readTypesFile file
  | isSuffixOf ".hs" file = do content <- readFile file
                               let ls = lines content
                               return $ filter isTypeSignature ls
  | otherwise             = return []

-- list children of directory, prepend directory name
qualifiedChildren path = do childs <- listDirectory path
                            return $ map (\name -> path++"/"++name) childs

readTypesDir :: FilePath -> IO [String]
readTypesDir path = do childs <- qualifiedChildren path
                       typess <- forM childs readTypes
                       return $ concat typess

-- read types contained in a file or directory
readTypes :: FilePath -> IO [String]
readTypes path = do isDir <- doesDirectoryExist path
                    if isDir then readTypesDir path else readTypesFile path

main = do ts <- readTypes "."
          mapM_ putStrLn ts

What does it all mean?

Let’s return to the functional world
putStrLn :: String -> IO () is a pure function that returns an operation
How is it pure? putStrLn x is the same when x is the same
In other words: an operation is a pure description of a chain of side effects
Only executing the operation causes those side effects
When a Haskell program is run, only one operation is executed
- It’s called main :: IO ()
- Other operations can be run only by linking them up to main
(Also, GHCi executes operations)

Prelude> let x = print 1   -- creates operation, doesn't run it
Prelude> x                 -- runs the operation
1
Prelude> x                 -- runs it again!
1

Operations are values

Operations are values just like numbers, lists and functions
Let’s write some code that operates on operations

choice :: IO a -> IO a -> IO a
choice a b =
  do putStr "a or b? "
     x <- getLine
     case x of "a" -> a
               "b" -> b
               _ -> do putStrLn "Wrong!"
                       choice a b

The C family of languages has a short-circuiting && operator, which is useful in the presence of side effects
Let’s write our own:

cand :: IO Bool -> IO Bool -> IO Bool
cand a b = do bool <- a
              if bool
                then b
                else return False

the side effects of b happen only if a returns True

Operations are values: more examples

Let’s implement the open-process-close idiom:

opc :: IO a -> (a -> IO b) -> (a -> IO ()) -> IO b
opc open process close = do
   resource <- open
   result <- process resource
   close resource
   return result

Now we can define:

firstLineOfFile path = opc (openFile path ReadMode) hGetFile hClose
withFile path op = opc (openFile path ReadMode) op hClose

Or using imaginary database functions:

connectDatabase :: IO Connection
execStmt :: Connection -> Statement -> IO Result
closeConnection :: Connection -> IO ()

execSqls :: [Statement] -> IO [Result]
execSqls stmts = opc connectDatabase (\conn -> mapM (execStmt conn) stmts) closeConnection

One more thing: IORef

The Haskell type IORef a is a mutable reference to a value of type a

newIORef :: a -> IO (IORef a)
readIORef :: IORef a -> IO a
writeIORef :: IORef a -> a -> IO ()
modifyIORef :: IORef a -> (a -> a) -> IO ()

Here’s an example of an imperative loop using IORef:

sumList :: [Int] -> IO Int
sumList xs = do r <- newIORef 0
                mapM_ (\x -> modifyIORef r (x+)) xs
                readIORef r

Using IORef isn’t necessary most of the time. Prefer recursion, arguments and return values
However real world programs might need one or two IORefs occasionally
There’s one exercise with IORefs, but otherwise IORefs shouldn’t be used in the exercises!

Summary of IO

A value of type IO X is an IO operation that produces a value of type X
Operations can be built using do-notation:

op :: X -> IO Y
op arg = do operation                 -- run operation
            operation2 arg            -- run operation with argument
            result <- operation3 arg  -- run operation with argument, store result
            let something = f result  -- run a pure function f, store result
            finalOperation            -- last operation produces the the return value

return x is the operation that always produces value x
Operations are pure values. Only running the operation causes the side effects

Oh right: tuples

Tuples or pairs (or triples, quadruples, etc) are a way of bundling a couple of values of different types together
The types are written like this: (a,b) and (a,b,c) and so on
Values are written like this: (1+1, True)
You can pattern match on tuples
You can use fst and snd on pairs:

fst :: (a, b) -> a
snd :: (a, b) -> b

For triples and so on, you need to use pattern matching

Tuples: examples

findWithIndex :: (a -> Bool) -> [a] -> (a,Int)
findWithIndex p xs = go 0 xs
  where go i (x:xs)
          | p x       = (x,i)
          | otherwise = go (i+1) xs

Prelude Data.List> :t partition
partition :: (a -> Bool) -> [a] -> ([a], [a])
Prelude Data.List> partition (>0) [-1,1,-4,3,2,0]
([1,3,2],[-1,-4,0])

Prelude Data.List> case partition (>0) [-1,1,-4,3,2,0] of (a,b) -> a++b
[1,3,2,-1,-4,0]

Lecture 5: fmap fmap fmap

Type classes
Evaluation

Type classes

How can Haskell’s + work on both Ints and Doubles?
Why can I compare all sorts of things with ==?

(+) :: (Num a) => a -> a -> a
(==) :: (Eq a) => a -> a -> Bool

The type (Eq a) => a -> a -> Bool means: for all types a that belong to the class Eq, this is a function of type a -> a -> Bool
A type class is a way to define operations that work on several different types
NB! a type class is a collection of types. It doesn’t have much to do with the classes of object oriented programming!
In some situations, type classes can act like interfaces in object oriented programming
Unfortunately the functions in a type class are often called methods, adding to the confusion

Type constraints

When you’re working with a concrete type (not a type variable), you can just use type class functions:

f :: (Int -> Int) -> Int -> Bool
f g x = x == g x

However in a polymorphic function, you need to add type constraints
This doesn’t work:

f :: (a -> a) -> a -> Bool
f g x = x == g x

Luckily the error is nice:

    • No instance for (Eq a) arising from a use of ‘==’
      Possible fix:
        add (Eq a) to the context of
          the type signature for:
            f :: (a -> a) -> a -> Bool
    • In the expression: x == g x
      In an equation for ‘f’: f g x = x == g x

This works:

f :: (Eq a) => (a -> a) -> a -> Bool
f g x = x == g x

Type constraints continued

If you don’t have a type signature, type inference can provide the constraints!

Prelude> let f g x = x == g x
Prelude> :type f
f :: (Eq a) => (a -> a) -> a -> Bool

You can have multiple constraints:

g :: (Eq a, Eq b) => a -> a -> b -> b -> Bool
g a0 a1 b0 b1 = a0 == a1 || b0 == b1

Example: `Eq` for a custom type

Here’s how to make your own type a member of Eq:

data Color = Black | White

instance Eq Color where
  Black == Black  = True
  White == White  = True
  _     == _      = False

Working with type classes

A type class is defined using class syntax. The functions in the class are given types:

class Size a where
  size :: a -> Int

Instances of a class are defined with instance syntax:

instance Size Int where
  size x = x

instance Size [a] where
  size xs = length xs

Working with type classes, continued

A class can contain multiple functions, and even constants:

class Foo a where
  empty :: a
  size :: a -> Int
  sameSize :: a -> a -> Bool

instance Foo (Maybe a) where
  empty = Nothing

  size Nothing = 0
  size (Just a) = 1

  sameSize x y = size x == size y

instance Foo [a] where
  empty = []
  size xs = length xs
  sameSize x y = size x == size y

Allowed instances

The Haskell 2010 standard only allows very limited type class instances:

instance Foo [a] -- this is ok
instance Foo [Int] -- this is NOT ok
instance Foo (Maybe a) -- this is ok
instance Foo (Maybe [a]) -- this is NOT ok

More specifically, only instances of the form instance MyClass (T a b..) are allowed, where T is a type constructor and a, b, … are different type variables.
There are widely used language extensionst that make more instances possible!

Default implementations

Type class functions can be given default implementations (compre: abstract classes in Java):

class Example a where
  example :: a
  examples :: [a]
  examples = [example]

instance Example Int where
  example = 1
  examples = [0,1,2]

instance Example Bool where
  example = True

class Combine a where
  combine :: a -> a -> a
  combine3 :: a -> a -> a -> a
  combine3 x y z = combine x (combine y z)

When you want to use the default implementation, just leave the function out of your instance declaration

Instance hierarchy

Both classes and instances can form hierarchies
Let’s start with a simple type class and instance

class Check a where
  check :: a -> Bool

instance Check Int where
  check x = x > 0

Now we can write a function that checks a list:

checkAll :: Check a => [a] -> Bool
checkAll = and (map check xs)

In order to turn this into a Check [a] instance, we need to add a constraint to the instance declaration:

instance Check a => Check [a] where
  check xs = and (map check xs)

Without the Check a => constraint, we get an error:

    • No instance for (Check a) arising from a use of ‘check’
      Possible fix:
        add (Check a) to the context of the instance declaration

(If you think about it, this is a way of circumventing the fact that we can’t make a Check [Int] instance)

Class hierarchy

Respectively, a class can depend on another class
This is useful when you want to use methods of another class in your default implementations:

class Foo a where
  foo :: a -> Int

class Foo a => Bar a where
  bar :: a -> a -> Int
  bar x y = foo x + foo y

More examples to come
Terminology: we say Bar is a subclass of Foo
- Note again the confusion with object oriented programming

Standard type classes: `Eq`, `Ord`

Eq is for equality, Ord is for comparisons
Note: all of the operations have default implementations in terms of each other
- This means you can pick which one is the easiest to implement when defining your instance

class  Eq a  where
      (==), (/=)  ::  a -> a -> Bool

      x /= y  = not (x == y)
      x == y  = not (x /= y)

class  (Eq a) => Ord a  where
  compare              :: a -> a -> Ordering
  (<), (<=), (>=), (>) :: a -> a -> Bool
  max, min             :: a -> a -> a

  compare x y | x == y    = EQ
              | x <= y    = LT
              | otherwise = GT

  x <= y  = compare x y /= GT
  x <  y  = compare x y == LT
  x >= y  = compare x y /= LT
  x >  y  = compare x y == GT

  max x y | x <= y    =  y
          | otherwise =  x
  min x y | x <= y    =  x
          | otherwise =  y

Example: the pair type

Here are the Eq and Ord instances for a simple type
Note that it is enough to define the <= operator for Ord due to the default implementations
- The term for this is minimal complete definition, often used in class documentation

data Pair a = MkPair a a
  deriving Show

instance Eq a => Eq (Pair a) where
  MkPair a b == MkPair c d  = a==c && b==d

instance Ord a => Ord (Pair a) where
  MkPair a b <= MkPair c d
     | a<c       = True
     | a>c       = False
     | otherwise = b<=d

*Main> (MkPair 1 2) < (MkPair 2 3)
True
*Main> (MkPair 1 2) > (MkPair 2 3)
False
*Main> compare (MkPair 1 2) (MkPair 2 3)
LT

Standard type classes: `Num`

The Num class contains normal arithmetic operations, plus a couple of weird ones
Haskell has other classes as well for numeric operations, see next slide
It’s a bit weird that Num needs Eq and Show…

class  (Eq a, Show a) => Num a  where
    (+), (-), (⋆)  :: a -> a -> a
    negate         :: a -> a
    abs, signum    :: a -> a
    fromInteger    :: Integer -> a

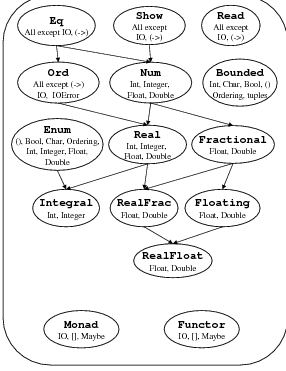
More standard type classes

Read: reading values from strings, read :: Read a => String -> a
Show: printing values as strings, show :: Show a => a -> String
Enum: for [x..y] syntax
Integral: various integer types: div, mod, toInteger
Fractional: division
Floating: floating point operations: exp, sin, pi…

Haskell 2010 type classes

`deriving`

The deriving syntax you’ve already seen is a way to generate automatic instances for a few basic type classes
- Read, Show and Eq most notably
The automatic instances are pretty straightforward
- show prints the value just like it would be in source code
- read reads values that show produces
- == compares all fields

All sorts of maps

Mapping, or changing a number of elements in one go, is a very common operation

mapList :: (a->b) -> [a] -> [b]
mapList _ [] = []
mapList f (x:xs) = f x : mapList f xs

mapMaybe :: (a->b) -> Maybe a -> Maybe b
mapMaybe _ Nothing = Nothing
mapMaybe f (Just x) = Just (f x)

data Tree a = Leaf | Node a (Tree a) (Tree a)

mapTree _ Leaf = Leaf
mapTree f (Node x l r) = Node (f x) (mapTree f l) (mapTree f r)

All sorts of functors

So let’s define a type class for types you can map over:

class Functor f where
  fmap :: (a->b) -> f a -> f b

This is actually straight from the standard library
NB! f is not a type but a type constructor
- Instances can be defined for type constructors in addition to (concrete) types
- In this case, the instance is for the type constructor so that the contained type can change from a to b
Instances of Functor:

instance Functor Maybe where
  fmap _ Nothing = Nothing
  fmap f (Just x) = Just (f x)

instance Functor Tree where
  fmap _ Leaf = Leaf
  fmap f (Node x l r) = Node (f x) (mapTree f l) (mapTree f r)

Functor is a class for types that behave like containers

List is a functor too

The list type constructor is written []:

instance Functor [] where
  fmap _ [] = []
  fmap f (x:xs) = f x : fmap f xs

How does Haskell work?

Here’s how a simple expression is evaluated in a C-like language, and in Haskell

not True = False
not False = True
map f [] = []
map f (x:xs) = f x : map f xs
length [] = 0
length (x:xs) = 1+length xs

In C-like langauges, function arguments are evaluated before the function:

length (map not (True:False:[]))
  ==> length (False:True:[])
  ==> 2

In Haskell, function arguments are evaluated lazily, as needed

length (map not (True:False:[]))
  ==> length (not True : map not (False:[]))
  ==> 1 + length (map not (False:[]))
  ==> 1 + length (not False : map not ([]))
  ==> 1 + 1 + length (map not [])
  ==> 1 + 1 + length []
  ==> 1 + 1 + 0
  ==> 2

A word about sharing

We discussed sharing structure in data structures some lectures ago
However any time you give a value a name, it gets shared:

f :: Int -> Int
f i = if i>10 then 10 else i

                  _______shared________
                 |                     |
f (1+1) ==> if (1+1)>10 then 10 else (1+1)
        ==> if 2>10 then 10 else 2
        ==> if False then 10 else 2
        ==> 2

You can name things via
- Function arguments
- let ... in ...
- where
So combined with laziness, this means that a name gets evaluated at most once

Pretty normal forms

Haskell evaluates nothing unless it has to
Evaluation is forced by pattern matching
Weak head normal form (aka WHNF) means an expression that can’t be evaluated at it’s top level
- Constructors: False, Just (1+1), 0:filter f xs
- Functions: (\x -> 1+x)
WHNF is basically something you can pattern match
For example here, we have to evaluate x to WHNF to know which branch to take:

case x of Foo y -> ...
          Bar w z -> ...

Pattern matching in function arguments works the same way
Primitives like (+) also force their arguments
And so does printing values (obviously)

Detailed example 1

not :: Bool -> Bool
not True = False
not False = True

(||) :: Bool -> Bool -> Bool
True || _ = True
_    || x = x

even x  =  x == 0  ||  not (even (x-1))

Note that || forces its left argument, but not its right argument (pattern matching)

This means that even forces its first argument:

|| forces x==0
x==0 forces x

even 2
==> 2 == 0  ||  not (even (2-1))
==> False   ||  not (even (2-1))
==> not (even (2-1))
==> not ((2-1) == 0 || not (even ((2-1)-1)))
==> not (  1   == 0 || not (even (  1  -1)))               -- (sharing)
==> not (  False    || not (even (1-1)))
==> not (not (even (1-1)))
==> not (not ((1-1) == 0 || not (even ((1-1)-1))))
==> not (not (  0   == 0 || not (even (  0  -1))))         -- (sharing)
==> not (not (   True    || not (even (0-1))))
==> not (not True)
==> not False
==> True

With this definition even would not have worked (infinite recursion):

even' x =  not (even (x-1))  ||  x == 0

Detailed example 2

Now we can really understand what’s going on in the infinite list example from lecture 2

    head (filter (>100) (map (3^) [0..]))
==> head (filter (>100) (map (3^) (0:[1..])))
==> head (filter (>100) ((3^0) : map (3^) [1..]))
==> head (filter (>100) (1 : map (3^) [1..]))     -- (>100) forces 3^0
==> head (filter (>100) (map (3^) (1:[2..])))
==> head (filter (>100) ((3^1) : map (3^) [2..]))
==> head (filter (>100) (3 : map (3^) [2..]))
==> head (filter (>100) (map (3^) [2..]))
-- taking bigger steps now
==> head (filter (>100) (9 : map (3^) [3..]))
==> head (filter (>100) (27 : map (3^) [4..]))
==> head (filter (>100) (81 : map (3^) [5..]))
==> head (filter (>100) (243 : map (3^) [6..]))
==> head (243 : filter (>100) (map (3^) [6..]))
==> 243

Lecture 6: A Monoid in the Category of Problems

Example 1: Maybes

When working with many Maybe values, the code tends to become a bit messy:

lookup :: (Eq a) => a -> [(a, b)] -> Maybe b

increase :: Eq a => a -> Int -> [(a,Int)] -> Maybe [(a,Int)]
increase key val assocs =
  case lookup key assocs
  of Nothing -> Nothing
     Just x -> if (val < x)
                then Nothing
                else Just ((key,val) : delete (key,x) assocs)

This type of code is pretty common, and usually repeats the same pattern:
- If any intermediate result is Nothing, the whole result is Nothing

Example 1: continued

So let’s define a chaining operator ?>
result + next step of computation ==> next result

(?>) :: Maybe a -> (a -> Maybe b) -> Maybe b
Nothing ?> _ = Nothing   -- if we failed, don't even bother running the next step
Just x  ?> f = f x       -- otherwise run the next step

increase key val assocs =
    lookup key assocs ?>
    check ?>
    mk
  where check x
           | x < val   = Nothing
           | otherwise = Just x
        mk x = Just ((key,val) : delete (key,x) assocs)

Example 2: more Maybes

Here’s a simple example of chaining with some list operations:

(?>) :: Maybe a -> (a -> Maybe b) -> Maybe b
Nothing ?> _ = Nothing   -- if we failed, don't even bother running the next step
Just x  ?> f = f x       -- otherwise run the next step

safeHead :: [a] -> Maybe a
safeHead [] = Nothing
safeHead (x:xs) = Just x

safeTail :: [a] -> Maybe [a]
safeTail [] = Nothing
safeTail (x:xs) = Just xs

safeThird xs = safeTail xs ?> safeTail ?> safeHead

safeNth 0 xs = safeHead xs
safeNth n xs = safeTail xs ?> safeNth (n-1)

safeThird [1,2,3,4]
  ==> Just 3
safeThird [1,2]
  ==> Nothing
safeNth 5 [1..10]
  ==> Just 6
safeNth 11 [1..10]
  ==> Nothing

Example 3: Logging

The type Logger represents a value plus a list of log messages (from the computation that produced the value)
Let’s use the same chaining idea as before

-- Logger definition
data Logger a = Logger [String] a  deriving Show
getVal (Logger _ a) = a
getLog (Logger s _) = s

-- Primitive operations:
nomsg x = Logger [] x        -- a value, no message
annotate s x = Logger [s] x  -- a value and a message
msg s = Logger [s] ()        -- just a message

(#>) :: Logger a -> (a -> Logger b) -> Logger b
Logger la a #> f = let Logger lb b = f a  -- feed value to next step
                   in Logger (la++lb) b   -- bundle result with all messages

-- compute the expression 2*(x^2+1)
compute x =
  annotate "^2" (x*x)
  #>
  \x -> annotate "+1" (x+1)
  #>
  \x -> annotate "*2" (x*2)

compute 3
  ==> Logger ["^2","+1","*2"] 20

Example 3: continued

A logging version of filter:

data Logger a = Logger [String] a  deriving Show

nomsg x = Logger [] x        -- a value, no message
annotate s x = Logger [s] x  -- a value and a message
msg s = Logger [s] ()        -- just a message

(#>) :: Logger a -> (a -> Logger b) -> Logger b
Logger la a #> f = let Logger lb b = f a  -- feed value to next step
                   in Logger (la++lb) b   -- bundle result with all messages

-- sometimes you don't need the previous value:
(##>) :: Logger a -> Logger b -> Logger b
Logger la _ ##> Logger lb b = Logger (la++lb) b

filterLog :: (Eq a, Show a) => (a -> Bool) -> [a] -> Logger [a]
filterLog f [] = nomsg []
filterLog f (x:xs)
   | f x       = msg ("keeping "++show x) ##> filterLog f xs #> (\xs' -> nomsg (x:xs'))
   | otherwise = msg ("dropping "++show x) ##> filterLog f xs

filterLog (>0) [1,-2,3,-4,0]
  ==> Logger ["keeping 1","dropping -2","keeping 3","dropping -4","dropping 0"] [1,3]

Example 4: keeping state

In the previous example we just wrote some state (the log)
Sometimes we want computation that depends on some state we are tracking
Simple example: number tree nodes left to right

data Tree a = Leaf | Node a (Tree a) (Tree a)

number tree = t
  where (t,i) = number' 0 tree

number' :: Int -> Tree a -> (Tree Int, Int)
number' i Leaf = (Leaf,i)
number' i (Node _ l r) = (Node i' numberedL numberedR, i'')
  where (numberedL, i')  = number' i l
        (numberedR, i'') = number' (i'+1) r

number (Node 0 (Node 0 (Node 0 Leaf Leaf) Leaf) (Node 0 (Node 0 Leaf Leaf) (Node 0 Leaf Leaf)))
     ==> Node 2 (Node 1 (Node 0 Leaf Leaf) Leaf) (Node 4 (Node 3 Leaf Leaf) (Node 5 Leaf Leaf))

Manually keeping track of the state is a bit painful

Example 4: … with chaining

Let’s see if we can define a chaining operator for this
We’re updating a state of type Int
This means functions of type Int -> (a, Int)
- a would be Tree Int in our example
Let’s define a type Counter a for this purpose

data Counter a = Counter (Int -> (a,Int))

runCounter :: Counter a -> Int -> (a,Int)
runCounter (Counter f) s = f s

-- Get the current state, increment the state by one
getAndIncrement :: Counter Int
getAndIncrement = Counter (\i -> (i,i+1))

-- Produce the given value, don't change the state
noChange :: a -> Counter a
noChange x = Counter (\i -> (x,i))

chain :: Counter a -> (a -> Counter b) -> Counter b
chain op f = Counter g
  where g i = let (value, new) = runCounter op i
                  op2 = f value
              in runCounter op2 new

-- query the counter two times
example = getAndIncrement
          `chain`
          (\val1 -> getAndIncrement `chain` (\val2 -> noChange (val1, val2)))

runCounter example 2 ==> ((2,3),4)

Example 4: continued

And now tree numbering with chain:

number :: Tree a -> Tree Int
number tree = t
  where (t,_) = runCounter (number' tree) 0

number' :: Tree a -> Counter (Tree Int)
number' Leaf = noChange Leaf
number' (Node _ l r) =
  number' l
  `chain`
  (\numberedL -> getAndIncrement
                 `chain`
                 (\i -> number' r
                        `chain`
                        (\numberedR -> noChange (Node i numberedL numberedR))))

number (Node 0 (Node 0 (Node 0 Leaf Leaf) Leaf) (Node 0 (Node 0 Leaf Leaf) (Node 0 Leaf Leaf)))
     ==> Node 2 (Node 1 (Node 0 Leaf Leaf) Leaf) (Node 4 (Node 3 Leaf Leaf) (Node 5 Leaf Leaf))

Finally: Monad

We’ve now seen three different types with a chaining operation:

(?>) :: Maybe a -> (a -> Maybe b) -> Maybe b
(#>) :: Logger a -> (a -> Logger b) -> Logger b
chain :: Counter a -> (a -> Counter b) -> Counter b

Just like before with map and Functor, there is a type class that captures this pattern:

class Monad m where
  (>>=) :: m a -> (a -> m b) -> m b

There are some additional operations in Monad too:

  -- lift a normal value into the monad
  return :: a -> m a
  -- simpler chaining (remember ##>!)
  (>>) :: m a -> m b -> m b
  a >> b  =  a >>= \_x -> b
  -- failed computation
  fail :: String -> m a

Don’t panic!

Functor was about a generic map operation:

fmap :: Functor f :: (a->b) -> f a -> f b

Monad is just about a generic chaining operation:
- in other words, about how we can take a monadic operation (m a) and do some further computation with its result (a -> m b).

(>>=) :: Monad m => m a -> (a -> m b) -> m b

If this feels too abstract, just recall how chaining works for Maybe:

(>>=) :: Maybe a -> (a -> Maybe b) -> Maybe b
Nothing >>= _ = Nothing  -- if we failed, don't even bother running the next step
Just x  >>= f = f x      -- otherwise run the next step

Maybe is a Monad!

Here’s the Monad instance for Maybe:

instance  Monad Maybe  where
    (Just x) >>= k      = k x
    Nothing  >>= _      = Nothing

    (Just _) >>  k      = k
    Nothing  >>  _      = Nothing

    return              = Just
    fail _              = Nothing

Here’s how it works:

Just 1 >>= \x -> return (x+1)
  ==> Just 2
Just "HELLO" >>= \x -> return (length x) >>= \x -> return (x+1)
  ==> Just 6
Just "HELLO" >>= \x -> Nothing
  ==> Nothing
Just "HELLO" >> Just 2
  ==> Just 2
Just 2 >> Nothing
  ==> Nothing

Maybe is a Monad! continued

Here’s the increase example rewritten with monad operations
The changes are ?> to >>=, Just to return and Nothing to fail

increase key val assocs =
    lookup key assocs >>=
    check >>=
    mk
  where check x
           | val < x   = fail ""
           | otherwise = return x
        mk x = return ((key,val) : delete (key,x) assocs)

The return of `do`

We can write nice code like this with monad operations

f = op1 >>= continue
  where continue  x   = op2 >> op3 >>= continue2 x
        continue2 x y = op4 >> op5 x y

Let’s inline the definitions:

f = op1 >>= (\x ->
               op2 >>
               op3 >>= (\y ->
                          op4 >>
                          op5 x y))

And indent weirdly:

f = op1 >>= \x ->
    op2 >>
    op3 >>= \y ->
    op4 >>
    op5 x y

The return of `do`: continued

On the last slide we came up with

f = op1 >>= \x ->
    op2 >>
    op3 >>= \y ->
    op4 >>
    op5 x y

Recall do notation:

f = do x <- op1
       op2
       y <- op3
       op4
       op5 x y

These are the same code!
Actually do is just a nicer way to write monad operations

The return of `do`: continued

Here’s how do notation gets transformed into monad operations
Note! the definition is recursive

do x <- op a       ~~~>       op a >>= \x -> do ...
   ...

do op a            ~~~>       op a >> do ...
   ...

do let x = expr    ~~~>       let x = expr in do ...
   ...

do finalOp         ~~~>       finalOp

More `do` examples

Here’s safeNth using do notation:

safeHead :: [a] -> Maybe a
safeHead [] = Nothing
safeHead (x:xs) = Just x

safeTail :: [a] -> Maybe [a]
safeTail [] = Nothing
safeTail (x:xs) = Just xs

safeNth 0 xs = safeHead xs
safeNth n xs = do t <- safeTail xs
                  safeNth (n-1) t

Here is increase one more time, with do notation:

increase key val assocs = do
    val <- lookup key assocs
    check val
    return ((key,val) : delete (key,x) assocs)
  where check x
           | val < x   = fail ""
           | otherwise = return x

Pretty nice, right?

Logger is a Monad!

Here’s the Monad instance for Logger
Note how nice filterLog is with do notation

data Logger a = Logger [String] a  deriving Show

instance Monad Logger where
  return x = Logger [] x
  Logger la a >>= f = Logger (la++lb) b
    where Logger lb b = f a

msg s = Logger [s] ()

compute x = do
  a <- annotate "^2" (x*x)
  b <- annotate "+1" (a+1)
  annotate "*2" (b*2)

filterLog :: (Eq a, Show a) => (a -> Bool) -> [a] -> Logger [a]
filterLog f [] = return []
filterLog f (x:xs)
   | f x       = do msg ("keeping "++show x)
                    xs' <- filterLog f xs
                    return (x:xs')
   | otherwise = do msg ("dropping "++show x)
                    filterLog f xs

filterLog (>0) [1,-2,3,-4,0]
  ==> Logger ["keeping 1","dropping -2","keeping 3","dropping -4","dropping 0"] [1,3]

The State Monad

Haskell’s State monad is a generalized version of our Counter type

data State s a = State (s -> (a,s))

runState (State f) s = f s

put :: s -> State s ()
put state = State (\_state -> ((),state))

get :: State s s
get = State (\state -> (state,state))

modify :: (s -> s) -> State s ()
modify f = State (\state -> ((), f state))

instance Monad (State s) where
  return x = State (\s -> (x,s))

  op >>= f = State h
    where h state0 = let (val,state1) = runState op state0
                         op2 = f val
                     in runState op2 state1

NB! State s is a type constructor because the second argument is missing
State represents computation with one global variable

State example 1

Here’s how you work with a counter in State

add :: Int -> State Int ()
add i = do old <- get
           put (old+i)

runState (add 1 >> add 3 >> add 5 >> add 6) 0
  ==> ((),15)

oo = do add 3
        value <- get
        add 1000
        put (value + 1)
        return value

runState oo 1
(4,5)

State example 2

A list state can replace an accumulator parameter

remember :: a -> State [a] ()
remember x = modify (x:)

valuesAfterZero xs = runState (go xs) []
  where go :: [a] -> State [a] ()
        go (0:y:xs) = do remember y
                         go (y:xs)
        go (x:xs) = go xs
        go [] = return ()

valuesAfterZero [0,1,2,3,0,4,0,5,0,0,6]
  ==> ((),[6,0,5,4,1])

State example 3

Checking for balanced parentheses:

parensMatch xs = v
  where (v,_) = runState (matcher xs) 0

matcher :: String -> State Int Bool
matcher [] = do s <- get
                return (s==0)
matcher (c:cs) = do case c of '(' -> modify (+1)
                              ')' -> modify (-1)
                              _ -> return ()
                    s <- get
                    if (s<0) then return False else matcher cs

Tree numbering:

number :: Tree a -> Tree Int
number tree = t
  where (t,_) = runState (numberer tree) 0
numberer :: Tree a -> State Int (Tree Int)
numberer Leaf = return Leaf
numberer (Node _ l r) = do numberedL <- numberer l
                           i <- get
                           put (i+1)
                           numberedR <- numberer r
                           return (Node i numberedL numberedR)

The return of `mapM`

The control structures from the IO lecture work in all monads
Here are their real types:

when :: Monad m => Bool -> m () -> m ()        -- conditional operation
unless :: Monad m => Bool -> m () -> m ()      -- same but flipped
replicateM :: Monad m => Int -> m a -> m [a]   -- do something many times
replicateM_ :: Monad m => Int -> m a -> m ()   -- same, but ignore the results
mapM :: Monad m => (a -> m b) -> [a] -> m [b]  -- do something on a list's elements
mapM_ :: Monad m => (a -> m b) -> [a] -> m ()  -- same, but ignore the results
forM  :: Monad m => [a] -> (a -> m b) -> m [b] -- mapM but arguments reversed
forM_ :: Monad m => [a] -> (a -> m b) -> m ()  -- same, but ignore the results

Examples:

safeHead :: [a] -> Maybe a
safeHead [] = Nothing
safeHead (x:xs) = Just x
firsts :: [[a]] -> Maybe [a]
firsts xs = mapM safeHead xs

firsts [[1,2,3],[4,5],[6]] ==> Just [1,4,6]
firsts [[1,2,3],[],[6]]    ==> Nothing

let op = modify (+1) >> get
    ops = replicateM 4 op
in runState ops 0
  ==> ([1,2,3,4],4)

The return of `mapM`: continued

Here’s filter reimplemented using the State monad:

sfilter :: (a -> Bool) -> [a] -> [a]
sfilter f xs = reverse $ execState (go xs) []
  where go xs = mapM_ maybePut xs
        maybePut x = when (f x) (modify (x:))

sfilter even [1,2,3,4,5]
  ==> [2,4]

Polymorphic Monad operations

We can write our own operations that work for all Monads
This is made possible by type classes, as discussed last week

mywhen b op = if b then op else return ()

mymapM_ op [] = return ()
mymapM_ op (x:xs) = do op x
                       mymapM_ op xs

*Main> :t mywhen
mywhen :: (Monad m) => Bool -> m () -> m ()
*Main> :t mymapM_
mymapM_ :: (Monad m) => (t -> m a) -> [t] -> m ()

Monads are Functors

One useful operation hasn’t yet been introduced: liftM

liftM :: Monad m => (a->b) -> m a -> m b
liftM f op = do x <- op
                return (f x)

liftM makes it easy to write code with pure and monadic parts:

liftM sort $ firsts [[4,6],[2,1,0],[3,3,3]]
  ==> Just [2,3,4]

Does the type of liftM look familiar?

fmap :: Functor f => (a->b) -> f a -> f b

It’s easy to define a Functor instance for a Monad: fmap = liftM!
All the standard library Monads are also Functors

fmap sort $ firsts [[4,6],[2,1,0],[3,3,3]]
  ==> Just [2,3,4]

One more Monad

The List Monad (that is, the Monad instance for []) represents computations with multiple return values
It’s useful for searching through alternatives
First example:

[1,2,3] >>= \x -> [-x,x]
  ==> [-1,1,-2,2,-3,3]

More interesting example: find all the pairs in a list that sum to k

findSum :: [Int] -> Int -> [(Int,Int)]
findSum xs k = do a <- xs
                  b <- xs
                  if (a+b==k) then [(a,b)] else []

Or in other words:

findSum :: [Int] -> Int -> [(Int,Int)]
findSum xs k = do a <- xs
                  b <- xs
                  if (a+b==k) then return (a,b) else fail ""

findSum [1,2,3,4,5] 5
  ==> [(1,4),(2,3),(3,2),(4,1)]

One more example

Finding the longest palindrome embedded in a string

substrings :: String -> [String]
substrings xs = do i <- [0..length xs - 1]
                   let maxlen = length xs - i
                   j <- [1..maxlen]
                   return $ take j $ drop i $ xs

palindromesIn :: String -> [String]
palindromesIn xs = do s <- substrings xs
                      if (s==reverse s) then return s else fail ""

longestPalindrome xs = head . sortBy f $ palindromesIn xs
  where f s s' = compare (length s') (length s)  -- longer is smaller

longestPalindrome "aabbacddcaca"
  ==> "acddca"

One more implementation

Here’s how the list monad works:

instance Monad [] where
  return x = [x]                  -- an operation that produces one value
  lis >>= f = concat (map f lis)  -- compute f for all values, combine the results

Surprisingly simple!

Oh right, IO

As you’ve probably guessed by now, IO is a monad

instance Monad IO where

However the implementation of IO is magical. You probably won’t learn anything by reading it.
True side effects fit the Monad pattern just like State and Maybe
As a bonus, you can use all the generic monad operations (mapM and friends) with IO

Monads: summary

The Monad type class is a way to represent different ways of executing recipes
- failure (Maybe)
- state
- nondeterminism (the list monad)
- IO
When M is a monad, values of type M a are operations that produce a result of type a
Monads are a design pattern and a library (mapM etc)
- Using common abstractions makes it easier to understand code
- Reading a State operation is easier than deciphering a complicated recursion with state
Everything you can do with monads, you can also do without them
- Exception: IO
- Using a monad often simplifies code
Warning: the internet is full of tutorials trying to explain monads using a simple analogy
- In my experience, this doesn’t work
- What works is using different monads and slowly getting used to the concept

Introduction to Functional Programming

Lecture 1: …and so it Begins

Contents

Administrative information

Course structure

Grading

Read these

Haskell

Some History

Running Haskell

Let’s start!

Expressions and types

Syntax of expressions

Syntax of types

The structure of a Haskell program

The structure of a Haskell program

How do I get anything done?

Conditionals

Example

Local definitions

Pattern matching

Examples

Recursion

Examples

More recursion

Examples

All together now!

A word about indentation

Indentation examples:

A word about purity

Working on the exercises

Lecture 2: Catamorphic

Contents

Guards

Guards: examples

Lists

List operations

Examples

A word about type inference and polymorphism

Examples of type inference

A word about type annotations

Functional programming, at last

More functional programming

Even more functional programming

Partial application

Partial application 2

The . operator

The $ operator

Lambdas

Functional style

More functional list wrangling examples

… and more!

Colon

Building a list

Pattern matching for lists

Consuming a list

Building and consuming a list

Building and consuming a list continued

Infinite lists

Laziness & Purity

Laziness Example

Lecture 3: You Need String for a Knot

Contents

Algebraic Datatypes: Introduction

Algebraic Datatypes: Fields

Algebraic Datatypes: Constructors

deriving Show

Example 1: Maybe I’m Amazed

Example 1: continued

Algebraic Datatypes: type parameters

Syntactic note

Example 2: Either you die a hero…

Example 2: continued

Algebraic Datatypes: recursion

Example 3: Let me list the ways

Example 4: Growing a tree

Example 4: continued

Algebraic Datatypes: Summary

Immutability

Path copying

The `.` operator

The `$` operator

`deriving Show`

Lecture 4: `RealWorld -> (a,RealWorld)`

Oh right: `case of`

`do` as thou wilt

`return`

`return` pitfalls

`do` and types

More on `<-`

Example: `Eq` for a custom type

Standard type classes: `Eq`, `Ord`

Standard type classes: `Num`

`deriving`

The return of `do`